�Z���^�[�������֑�w�Q���w���܂Ł@��w���w�w���i���Z���Ώہj�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Q�����R�s
 �@�@
�@�@
���L�E�\��\
��{���
�m�̏��
��{���
�m�̏��
�Q�O�P�T�@�T��
�T���P���@�i�H�ɂ���
�f�v�𗘗p���ē�������F�l���A�Ȃ��Ă��āA�F�X�Șb������@�����܂����B���̗F�l�͈ꕔ����Ƃœ����Ă���̂ł����A����b���Ă��ċ����[�������̂́A�ނ̑�w�i�w�Ɏ���o�܂ł����B
�ނ͍��Z�P�N���̎��ɐe�Ɛi�H�̘b�����āA�w���d����Ȃǂ��l����Ɠ����ɍs���̂͂�߂Ăق����B�����āA�o�����������w�ɍs���Ăق����Ƃ������Ƃ�����ꂽ�����ł��B
�ނ́A�s��ɏo�čs�������Ƃ����v�����������̂ŁA�����ȊO���ƁA���A���É��A�����ɍs�������Ƃ����Ƃ��납���w���i�荞��ŁA���̓s�s�ɂ��鍑������w�̒��Ŏ������s����\���̂����w���l���܂����B�������x�ׂ�ƁA�Z���^�[���E�Ŏł����w���������̂ŁA���p���邱�Ƃ��l���ĕ]����グ�邽�߂ɒ���l���ƒ�o���ɗ͂�����ĕ������Ă����悤�ł��B�����Ĕނ́A�Z���^�[�����ŖڕW�Ƃ��Ă����_�������A�Z���^�[���E�ō�������w�ɓ��w���܂����B
�������ǂ̂悤�ȓ��ɐi�݂������Ƃ����ڕW�����Ƃ������Ƃ͑�Ȃ̂ł����A�̌o���̂Ȃ����Z�����ڕW�𗧂Ă�Ƃ��ɓ���̂́A�����̔\�͂͂ł��邩�ǂ����ł��B�ނ̂������Ƃ���́A�����̗͂�c�����ė�ÂɖڕW�ݒ肵�Ă����_�ł͂Ȃ����Ǝv���܂��B
�ڕW�����ĂƂ����Ă��A�����l���Ă悢�̂������炸�i�H�̕����������܂�Ȃ����Z�P�N���́A�e�̈ӌ����Ă݂邱�Ƃ������̍l����[�߂邫�������ɂȂ邩������܂���B
�ނ̘̎b���Ă�������������Ƃ�����܂��B
���̓C���^�[�l�b�g�̕��y�Ȃǂ�����A���邱�Ƃ͂���Ȃɓ������܂��A�Q�O�N�قǑO�͏��ɓ���h������ł����B���̎���ɁA��L�̂悤�Ȏ��g�ݕ����o�����̂́A�ނɔN�̗��ꂽ�Z�킪�������Ƃ��v���̈���Ǝv���܂��B���ɓ���ɂ��������n���ŁA�L�v�ȏ��������炵�Ă����Z�킪�������Ƃ͔ނɂƂ��čK�^�������Ɗ����܂��B
����ł́A���邱�Ƃ�������I�ʂ��邱�Ƃ�����Ȃ�܂����B�Z���^�[���E�Ɍ��炸�A�ɂ��Ă̏����ȒP�ɓ�����悤�ɂȂ�܂������A���������ɓK���Ă��邩�������邱�Ƃ͍���ł��B�ł����獡�A��ɂ��Ȃ��Ƃ����Ȃ����Ƃ͏��ɗx�炳��Ȃ��Ƃ������Ƃ��Ǝv���܂��B
�̑�O��Ƃ��Ĉ�ԑ�Ȃ̂́A�{���̗͂�����Ƃ������Ƃł��B�������Ȃ�������ɂ��āA�����̏��ɔ�т��Ȃ��悤�ɂ��Ă����������̂ł��B
�T���Q���@�l�R
�m�̌��ւ⒓�ԏ�ɂ悭�l�R�����āA����������Ɖ������瑖���Ċ���Ă��܂��B
���ɂ������Ǝv���Ă�����N�ɂł�����Ă���炵���A�m�������ɂ������Ă���݂����ł��B
���ꂾ���x���S���Ȃ��l�R���߂��炵���Ƃ������炢�A�����܂���B
�m���J������A�|�������Ă��鎞�͊��C�̂��߂ɔ����J���Ă���̂ł����A���������ւł��[���Ƃ�������f���Ă��܂����B
���ƒ������܂ɒ����̂����Ă���̂ŁA���̂����������ǂ��l�R�ɂȂ邩������܂���B

�T���R���@���̃T�C�N��
�����̂��߂��Ƃ������Ƃ�����A�f�v�𗘗p���Č��O�ɉ����ɍs��������������悤�ŁA���Ƃɏo���Ȃ����k�����܂��B���m�ł́A���O�Ɏ��ƂɎQ���ł��Ȃ����k�����邱�Ƃ��������Ă���A���Ƃ�i�߂��ɉ��K�╜�K�����邱�Ƃ������ł��B
���ݏm�ł́A�Q�N���͐��w�U�u�O�p���̉��@�藝�v�܂ŁA�R�N�����n�͐��w�V�u�ϕ��̌v�Z�v�܂Ŏ��Ƃ��I������̂ł����A�������Z�ł͂ǂ���̊w�N�����̕���ɓ����Ă��܂���B���e��蒅�����邽�߂ɕ��K�����Ȃ��Ƃ����Ȃ��ƍl���Ă����̂ŁA�f�v�͂����@��ɂȂ�܂����B
���̊��ԁA�������ŏm�ɗ���Ȃ����k�ɂ́A���O�Ƀv�����g��n���ďo����������Ă����悤�Ɏw�����o���Ă��܂��B��肫��Ȃ�������A������Ȃ������Ƃ���́A�ʎw���őΉ����Ă����\��ł��B
���͂�t���邽�߂ɂ́A�w�K�������e��Y��Ȃ����x�Ɏ��Ԃ��āA���x���������K������K�v������܂��B����܂����A���z�I�ȕ��̃T�C�N����
�m�ŗ\�K�@���@�w�Z�̎��Ƃ���@���@�w�Z�̉ۑ�ŕ��K�@���@�m�ŕ��K�@���@����l���O�Ɏ����ŕ��K�@���@�w�Z�̒����x�ɂ̉ۑ�ő����K
�Ƃ����悤�Ȃ��̂ł��B����́u�m�ŗ\�K�@���@�w�Z�̎��Ƃ���v�̊��Ԃ������Ȃ肷���邽�߁u�m�ŕ��K�v��O�|�����āA�T�C�N��������Ȃ��悤�ɂ���\��ł��B
�m�ɒʂ��Ă��Ȃ����k�́u�m�Łv�̕������u�����Łv�ɒu�������Ă݂�Ƃ悢�ł��傤�B�������A�u�����Łv�����܂ŊǗ��ł��鐶�k�́A���Ȃ��̂ł͂Ȃ����Ǝv���܂��B
�{���́A�ǂꂭ�炢���Ԃ������ĉ��炢���K������悢�̂����A���k���������g�ōl���Ď��s�ł��邱�Ƃ����z�ł��B�������A�������o����������Ώ�肭�o���܂���B�f���̂��鐶�k�ł����Ă��A���������̎d�����o���Ă���Ƃ͌���܂���B�n�߂͂�����Ńy�[�X���C�N���邱�ƂŁA���̎d�����`���Ă��������Ǝv���Ă��܂��B
�T���T���@�ē�
�f�v���̑�w���͎��Ԃ�����悤�ŁA�w�Z����̋����q�����Ɍ�����K�˂Ă��Ă���܂����B
�������点�������������A�H�ׂ������̂�����Ή��ł������Ȃ�ƕ�������
��҂炵��
�u�ē����H�ׂ����ł����I�I�v
�ƁA�͂����蓚���Ă���܂����B
�����܂ł͂�����ƌ����Ă��炦��ƓX��I�ԑ��͂ƂĂ��y�ł��B
���������Ȃ̂ŁA���R�ł��l�C�̓X�ɘA��čs���Ă����܂����B
�w�Z���m���܂߂āA���Ƃ������k�ƊW�������Ă������Ƃ͓�����O�ł͖����A�������ĐH���ɍs���Đ��������p��������̂͂ƂĂ��K���Ȃ��Ƃ��Ɗ����܂��B

�T���U���@�Q�l��
��N�A�m�ɍݐЂ��Ă������k���f�v�x�ɂ𗘗p���ĉ�ɗ��Ă���܂����B
��ɂ��Ă��ꂽ���k�́A���N�̂Q���ɋ��s��w�������̂ł������i�Ȃ炸�A�Q�l���邱�Ƃ�I�����Č��݂͌��O�̗\���Z�ɒʂ��Ă��܂��B
���̏m�ł͊�{�I�ɘQ�l���̎���͍s���Ă��܂���B�Q�l������̂ł���A�P�Ȃ̏m�ɍs�������\���Z�ɍs�������{�l�̂��߂ɂȂ�ƍl���Ă���̂ŁA���̂悤�ɂ����߂��܂��B���ɓ�֑�w��ڎw���ĘQ�l����Ƃ��́A�S�����̗\���Z�ɍs���A�P�N�Ԋ撣��������i�̉\���͐�ɍ����Ȃ�Ǝv���܂��B
�\���Z�ɍs�������b�g�́A�S�Ȗڂ����Ă��炦��Ƃ������Ƃ�����܂����A���Ԃ��Ǘ����Ă��炦�邱�ƁA����ɓ��l�ɘQ�l���Ă���l�����邱�Ƃ������傫���Ǝv���܂��B�����͎̂������g�ōs�����̂ł����A�P�N�ԁA��l�����Ńy�[�X����������������邱�Ƃ͍���ł��B�������ԁA���ɏW�����邽�߂ɂ́A���_�I�ȕ��S���y�����邱�Ƃ��K�v�ɂȂ�܂��B
����́A���A�����ł͂Ȃ��A�\���Z�ŕ������Ă��āA�ǂ����Ă������ł��Ȃ��Ƃ���̎�������˂ĉ�ɂ��Ă���܂����B�v���Ԃ�Ɉꏏ�ɕ��ł��āA�y�������Ԃ��߂����܂����B

�T���V���@���݂₰
����A�����Ɠ��L�ɏ����Ă������Ɛ������͂ƂĂ��C���g����l�����ŁA���݂₰���Ă��Ă���܂����B
�Ə����ƁA��ɗ���Ƃ��͂��݂₰�������Ă��Ȃ��Ƃ����Ȃ��Ɗ����鑲�Ɛ������邩������Ȃ��̂Ō����Ă����܂����A��Ԃ�ŗ��Ă�����đS�R�\���܂���B
�����Ă��Ă��ꂽ���݂₰�́A���R�ɂ��܂̐F�܂œ����ŁA�ǂ�����������̂��邨�َq�ł����B���Ƃ����Ă���ƁA�����ԐH�������Ȃ����Ƃ������̂ŁA�ƂĂ�������܂��B
�����J���Ă݂�ƁA���b�s���O�Ɏ���G�܂ŕ`���Ă���Ă��܂����B�����ł͐�Ɏv�����Ȃ����o���Ȃ����Ƃ�����Ă��炦��Ɗ��������̂ł��ˁB

�T���W���@�v�Z�������Ɩ�萳�����̊W
���w�ɋ���������l�́u��w�ւ̐��w�v�Ƃ����G����m���Ă���Ǝv���܂����A�������̓��e�ŁA�v�Z�����������萳�������l����Ƃ����b�������Ă���܂����B�ʔ������e�ł��̂ŁA�����ŏЉ���Ă��炢�����Ǝv���܂��B
�G�������̂܂܂Ƃ����킯�ɂ������܂���̂ŁA�v�Z�������Ɩ�萳�����̊W�\���쐬���Ă݂܂����B
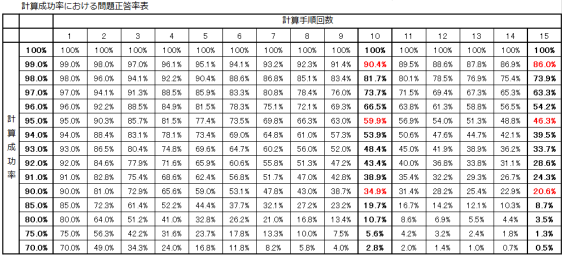
���[�̐��l���A�v�Z�ň�̎菇�𐬌�����m����
��[�̐��l���A���̎菇�����s�����\���Ă��܂��B
��L�̕\����
��̎菇���X�O����������ꍇ�A�P�O����s����ΐ������͖�R�T��
��̎菇���X�T����������ꍇ�A�P�O����s����ΐ������͖�U�O��
��̎菇���X�X����������ꍇ�A�P�O����s����ΐ������͖�X�O��
�Ƃ������Ƃ��ǂݎ��܂��B
���w���̂Ƃ��Ɏ�舵�����́A�W���I�Ȍv�Z�ł���Ύ菇�̉�����قǑ�������܂���B���̂��߁A�v�Z�������ɑ��Ă̐������̌��蕝�����Ȃ����߁A�����̌v�Z�̖͂����ɋC�Â��Ă��Ȃ��l�����邩������܂���B
�������A���Z�ŏo�肳�����̌v�Z�́A�菇�̉����Ȃ葝�����܂��B���ɍ��Z�R�N�����n���s���ϕ��v�Z�͕W���I�Ȃ��̂ł��菇���P�O���Ă��܂��B����́A��̎菇���X�X���ԈႦ�Ȃ��悤�Ȑl�ł��P�O��ɂP��͊ԈႦ��Ƃ������ƂŁA����Ȃ��v�Z���������P�O�O���ɋ߂��Ȃ�悤�ɗ��K���Ȃ���A���肵���_���͖]�߂Ȃ��Ƃ������Ƃ��Ӗ����Ă��܂��B
�v�Z���K�œ��������킹��悤�Ȓ����������Ă���ƁA�v�Z�������͒��X�オ��܂���B�����������ɑΉ��ł���悤�ɂȂ邽�߂ɂ͒��w���⍂�Z�P�N���̂Ƃ�����A�ӎ������Čv�Z���������グ�Ă����K�v������܂��B
�����͂ǂ��łǂ̂悤�ȊԈႢ�������Ă���̂��m�F���Ȃ��甽�����K���s���A�P�O�O����ڎw���ēw�͂��Ȃ���Ȃ�܂���B
�T���X���@�ł����R�N���ɂȂ�Ȃ����߂�
���݂P�N���X�̒���͂P�Q���ƂȂ��Ă��܂����A�S���ɓ��m�����R�N���������A�R�N�����n�N���X�͎c�Ȃ��P�ƂȂ��Ă��܂��B�N���X��l���𑝂₹������̂ł����A����ł͂��܂葽���̐��k������邱�Ƃ��ł��܂���B����́A���Ǝ��Ԃ�P�x�ɋ�������l���̌��E�ʂ̑��ɁA�ʎw���Ɏg���鎞�Ԃ�����Ȃ��Ȃ�Ƃ������R����ł��B
�܂Ŏ��Ԃ̂���P�A�Q�N���Ƃ͈Ⴂ�A�R�N���̓Z���^�[�����܂Ŏc��Q�T�O�����x�ɂȂ�A�����_�ŏł�������Ă��鐶�k�������悤�ŁA�ʎw����\������ł��鐶�k�̐��������Ă��܂��B
�o�������Ή����Ă�������悤�ɓw�͂����Ă��܂����A���m�͂����܂ł����Ƃ����C���ł��̂ŁA�S���̊�]�ʂ�̎��ԂɌʎw�������Ă����邱�Ƃ��o���Ȃ����Ƃ�����܂��B���Ƃŋ��Ȕ͈͂̕��K���s����悢�̂ł����A�R�N�����n�͐��w�V�̉��K�ʂ��m�ۂ��邽�߂ɕ��K�������Ă���킯�ɂ������܂���B
���̂悤�ȏ̒��A�R�N�����n�ŕ��K���Ă���͈͂��R�N�����n�̃A�i�E���X���āA��]���鐶�k�͈ꏏ�Ɏ��Ƃ��Ă��炤�悤�ɂ��܂����B�V���܂łɋ�蕪���ׂ��Ă����Ȃ��Ɩ{�i�I�Ȗ�艉�K�ɓ��邱�Ƃ��o���Ȃ����߁A���撣���Ă����Ăق����Ǝv���܂��B
���̂悤�Ɍʎw������Ƃ�D������āA�R�N������̓��m�ł��o�������̑Ή������܂����A���k�̕��S�͂��Ȃ�傫�Ȃ��̂ƂȂ�܂��B�P�A�Q�N���̂�������ʏm������A�]�T�������ĂR�N�����}������悤�ɂȂ�܂��̂ŁA�ӗ~�̂���l�͑��߂̍s�����Ƃ��Ă��炢�����Ǝv���܂��B
�T���P�O���@�⏕
�̑��I��̗��K�œ�Փx�������Z�ɗ��K����Ƃ��ɁA�⏕������l�����Ă���̂����邱�Ƃ�����܂��B
������������A�D�G�ȑI��́A�n�߂���Z�̃C���[�W��N���Ɏ����Ƃ��ł��ĕ⏕��K�v�Ƃ��Ȃ��̂�������܂��A�قƂ�ǂ̑I��́A�V���ȋZ�̓�����̂Ɋo�������邽�߂ɕ⏕�����Ă�����Ă���̂ł͂Ȃ��ł��傤���B
���ł������悤�Ȃ��Ƃ��K�v���Ǝv���܂��B�R�N���̗��n�͌��݁A�ϕ��@�̉��p�̎��Ƃ��s���Ă���̂ł����A����܂ł̊�{�v�Z�����Փx���O�b�Əオ���Ă��܂��B
���w�̊�����������Ă��鐶�k�͓�Ȃ��������Ă����̂ł����A�����������Ă悢�̂��킩��Ȃ��Ƃ������k�̕��������I�ɑ����悤�Ɋ����܂��B
�������A�S�Ă̖����P����S�Đ������Ă��܂��ƁA�ǂ̕����Ŏ����͈����������Ă��邩������Ȃ�������A�l����͂��t���Ȃ������肵�܂��B�ł��̂ŁA���݂́A��{�I�ɂ͐��k�ɖ����������āA�������菕������悤�Ȏ��Ƃ��s���Ă��܂��B
�w���͓�����̂ŁA���ׂč��ؒ��J�ɍs���悢�Ƃ������̂ł�����܂���B���k�̏����āA�ǂ��܂Ŏ菕�����邩�f����̂��w���҂ɋ��߂��鎑�����Ǝv���܂��B
�T���P�P���@��
����́A�m�Ŏg���Ă��鎆�̉摜�ł��B

�R�s�[�p���͒ʔ̂ōw�����Ă���̂ł����A�E�����ȑO�̂��̂ŁA��������w���������̂ł��B�l�i���قړ����������̂Ő[���l�����ɔ��������Ƃ���A�ȑO�܂łƈႤ�p���ɂȂ��Ă��܂��܂����B
����������Ďv�����̂ł����A�ȑO�g���Ă������̕������Ɍ����Ă���Ɗ����܂��B���������͐F���̖��Ȃ̂��A���̕������₽�瓧���Ă��܂��܂��B����ƁA�����������Ƃ��̃V���[�y���̈�������������ȑO�̎��̕����ǂ��悤�Ɋ�����̂ł��B
�l���猩��ǂ��ł��ǂ��悤�Ȃ��Ƃł����Ă��A�����̒��ŗ��R������A�������������đI�����Ă��������ƍl���Ă��܂��B������������ł��A�K���ɑI��ł͂����Ȃ������Ȃ��ƁA���Ȃ��܂����B
�T���P�Q���@�č\�z
���݁A���Z�R�N�����n�̎��Ƃ́A���k�̊�]�Łu�����v�̎��Ƃ����Ă��܂��B
�V�ے��̐��w�`�ɂ�����u�����v�̕���ɂ��ĐF�X�Ə����Ă��܂������A���Ȃ�Ɋ����Ă��邱�Ƃ�������x�����Ă��������Ǝv���܂��B
�܂��A���̕�����K���̂͂قƂ�ǂ����Z�P�N���̂Ƃ��Ȃ̂ł����A���̒i�K�Ŋ��S�ɗ������邱�Ƃ͓���̂ł͂Ȃ����Ǝv���܂��B
�����̐����͒P���Ȃ悤�œ���A�v�Z�����ŏ����ł��Ȃ��悤�Ȗ�肪�����̂ł��B�܂��A�u�ꍇ�̐��E�m���v�Ɍq����悤�ȍl���������邱�Ƃ�����A�����I�Ȑ��w�͂�����镪��̂��߁A���̕���̏K�n�x������x�ɊW���Ă��܂��B
���ɁA������ƁA��r�I�Ղ�����肪���݂��Ă��āA�������Â炭�����Ă���Ƃ�������������܂��B��ʓI�Ȗ��W��Q�l�����������A��肪�n�����ĂĐ�������Ă͂�����̂́A�w�K�̏��ԂɓK�����z�u�ɂ͂Ȃ��Ă��Ȃ��悤�Ɋ�����̂ł��B
�ȏ�̂悤�Ȃ��Ƃ�O�X���犴���Ă����̂ŁA����u�����v�̕���̎��Ƃ�����ɂ������āA���k���������₷���悤�ȏ��Ԃɓ��e��g�ݑւ����v�����g���쐬���邱�Ƃɂ��܂����B�u���l���v�Ɓu�ؖ����v�̂Q�ɕ����āA��r�I���g�݂₷���u���l���v����w�K��i�߂Ă����܂��B
�v�����g���쐬���Ă��ĉ��߂Ċ������̂ł����A�P�̕���̊w�K�v��𗧂Ă邱�Ƃ́A���̕����[����������菕���ɂȂ�܂��B���̎��Ƃ̗\�K�����łȂ��A�����狳���镪����܂Ƃ߂ė\�K���邱�ƂŁA�P�P�̎��Ƃ̎����オ���Ă���̂ł͂Ȃ����Ǝv���܂��B

�T���P�S���@�O���t�̕`����
���Z�P�N���̎��Ƃ���������Q�����̃O���t�ɓ���܂����B���N�͕��K�̎��Ԃ𑽂�����Ă��邽�߁A���Ƃ̐i�x�͏����x�߂ŁA�������Z��菭���������x�ƂȂ��Ă��܂��B
�O���t�͈̔͂ɓ���Ƃ��悢��A���Z�̐��w�炵���Ȃ��Ă��܂��B
���w�Z�܂łƂ̈�Ԃ̈Ⴂ�́A�O���t�̎��������ŕ`���Ȃ��Ƃ����Ȃ��_�ł͂Ȃ����Ǝv���܂��B���R�A�ڐ���������̂ŁA�ڕ��ʂŃO���t��`�����ƂɊ����K�v������܂��B
�܂��A�O���t��`�����߂̍Œ���̍�@�Ƃ������A���[����g�ɕt���Ȃ��Ă͂����܂���B���K������O�ɁA�ǂ��ɋC�����ăO���t��`���Ȃ��Ƃ����Ȃ��̂����A������Ɨ������Ă��Ȃ��ƁA�Ԉ�����O���t�����`���܂���B
���������߂��̐S�Ȃ̂ŁA���̏ꍇ�A���̂悤�ȓ����̎��Ƃłׂ͍�����@��`���āA���H�ł��Ă��邩��K���S���m�F����悤�ɂ��܂��B�������A�����ɋC������悤�ɂƌ���������ɊԈ���Ă��鐶�k�����܂����B����������@�́A�J��Ԃ����ӂ���Ĉӎ����Ȃ��Ă͐g�ɕt���Ȃ����̂Ȃ̂ŁA�n�߂͊Ԉ���Ă��Ă��S�R�\���܂���B
�O���t���K���n�߂��Ƃ��́A�w���҂Ɍ��Ă����Ȃ��ƍ����Ă��邩��������Ȃ��Ǝv���̂ŁA�m�ɒʂ��Ă��Ȃ��l�́A�w�Z�̐搶�Ɏ���I�Ɍ��Ă�����Ċm�F����̂��ǂ��Ǝv���܂��B
�T���P�T���@�ɂǂ��������Ă�����
���Z�R�N���̒��ɂ͊�@���������Ă��鐶�k�����Ȃ��炸���܂��B
��@���������邱�Ƃ͈������Ƃł͂Ȃ��̂ł����A�ł��Ă��܂��āA�F�X�Ȃ��̂Ɏ���o���Ȃ��悤�ɂ��Ȃ��Ă͂����܂���B
�܂ł̎c��������l������A���ꂩ��{�Ԃ܂łɂǂꂾ���̂��Ƃ��o����悤�ɂȂ�̂��낤���Ƃ����C�ɂȂ��Ă��܂��B����͐��k�����ł͂Ȃ��A�w���҂̑��ɂ��������Ƃ������܂��B���z�������A�S�Ă̖�肪������悤�ɂȂ��Ăق����Ƃ͎v���܂����A�Ȃ��Ȃ�����Ȃ킯�ɂ������܂���B
�m�ɗ��Ă��邩��ɂ́A�����ł���悤�ɂ��Ă����Ȃ��Ă͂����Ȃ��Ƃ����v��������܂��B�������A�ڂ̑O�̓_���ɂ�����������āA�\�ʓI�ȕ������������Ȃ��Ƃ����v��������܂��B
���Z�ƈႢ�A��w�ł́A�S�ẲȖڂ����S�Ɏd�オ������ԂŎł��鐶�k�͂���Ȃɑ�������܂���B���Ԃ������Ă���Ƃ����̒��ŁA�������I�ɑ����āA�ǂ̂悤�Ȏ��g�ݕ�������̂��A�����������Ƃ��ꏏ�ɍl���Ă�������悤�Ȏw�������Ă��������Ǝv���Ă��܂��B
�T���P�U���@�ӊO�Əo���Ȃ��A�o���Ă�����܂��̂���
�����A�P��e�X�g��������A���O�̗��������̐��k���������܂����B
�o���Ă��邤���ɋ}���ŒP����������Ɖ����n�߂����߁A�����Ă��Ȃ������̂��Ǝv���܂��B
�܂��A���O�������Ă��Ă��A�c�������ł�������A�Ђ炪�Ȃŏ����Ă��鐶�k�����܂����B�m�̒P��e�X�g�����炱�ꂭ�炢�ŗǂ��Ǝv���Ă���̂�������܂���B
�����������Ƃ͐F�X�Ƃ���̂ł����A���O�͈�ԏ��߂ɁA�t���l�[���ŁA�����ł���Ί����ŁA�����悤�ɏK���Â��������̂ł��B
�C�ɂȂ邱�Ƃ������ЂƂA�m�ɗ����Ƃ��ƋA��Ƃ��͈��A��������Ƃ���悤�Ɍ����Ă��܂����A�m�ɒʂ��Ďb���o�ƁA�����������܂܁u���悤�Ȃ�v�Ə��������ł����Ȃ���A�鐶�k�����܂��B
���̓s�x���ӂ��܂����A�����������Ƃ͕��ȑO�̖��ŁA������܂��ɏo���Ȃ�������܂���B
���m�́A�����������ł�������Ƃ͎v���Ă��܂���B�o���Ă�����܂��ƌ����邱�Ƃ��A���R�ɏo����悤�Ȑl�ɂȂ��Ăق����Ǝv���Đڂ��Ă��܂��B
�T���P�W���@���Z������ƁA���w���o����悤�ɂȂ邩������Ȃ�
�v�Z�~�X�̏��Ȃ����k�́A���̒��Ō��Z�����Ċm�F���Ȃ�����������i�߂Ă����K�������Ă��܂��B�t�ɁA�v�Z�~�X������܂���ƌ����Ă��鐶�k�́A���Z�̏K�������Ă��Ȃ��̂��Ǝv���܂��B���k�����������Ă���Ƃ�������Ă���ƁA�����Ă��Ȃ��Ă��A���̒��Ō��Z���s���Ă��邩�ǂ���������܂��B
���k�����Ă��Ďv���̂ł����A���Ƃ͌v�Z�~�X�̗ʂ����ɂƂǂ܂炸�A���Z������Ƃ����K�������w���o����l�Əo���Ȃ��l����v������Ȃ��̂��Ɗ����܂��B
���Z������Ƃ������Ƃ́A�����̍s���̊m�F��Ƃ��������g�ōs���Ƃ������Ƃł��B���̍s�ׂ��ᔻ�I�v�l��{�����A�����������āA�����Ԉ���Ă���̂����l����͂��t���Ă���A�Ƃ����̂͌����߂��ł��傤���B
�܂��A���Z��s���Ƃ������Ƃ́A�{���ʓ|�ȍ�Ƃł��B�����o����悤�ɂȂ邽�߂ɂ́A�ʓ|�Ɋ�����ł��낤�������K���s��Ȃ���Ȃ�܂���B�����������_�ł��A���ɑ���p���Ɍq����Ƃ��낪����̂�������܂���B
�w�������鑤�́A���̉�������l�����������邱�Ƃ͓��R�Ȃ̂ł����A���̂悤�ȁA���ւ̎��g�ݕ���`���邱�Ƃ���ł͂Ȃ����ƍl���Ă��܂��B
�����A���Z�����Ȃ�������i�߂�悤�Ɏw�������Ă��A�قƂ�ǂ̐��k�͂Ȃ��Ȃ����H���Ă���܂���B�꒩��[�ɕω����Ȃ��Ƃ������Ƃ͕������Ă���̂ŁA���C�����w�����Ă��܂��B���Ԃ͂������Ă��A�m�ɒʂ��Ă��鐶�k�ɂ͌��Z�̏K����g�ɕt���Ă��炢�����Ǝv���܂��B
�T���P�X���@�Ă̏���
���ꂩ����m���鐶�k������ΕύX���邱�Ƃ�����̂ŁA���̏�Ԃł����A�m�̃X�P�W���[���͂W�����܂ŏo���Ă��܂��B
���ł����Ă��A���̎����ɂW���܂ł̃X�P�W���[����g�ނ̂͗��R�������āA�X�P�W���[����������x���߂Ă��܂�Ȃ��ƁA���ނ��쐬�ł��Ȃ��̂ł��B
���Z�Q�N���܂ł́A�܂��K���Ă��Ȃ��͈͂�����̂ŁA�s�̂���Ă��鋳�ނ����C���Ɏw�����܂����A���Z�R�N���͂��ꂩ��̎����A�{�i�I�ȉ��K���s���܂��B�g�p���鋳�ނ́A���k�̐i�w��A�\�͂Ȃǂ��l�����āA���k�ɍ��������̂��쐬���Ă��܂��B
���̂�������쐬���Ă����Ȃ���A�V�����{����W�����܂ł͎��Ƃɐ�ڂ��Ȃ��Ȃ邽�߁A�]�T���������w�����ł��Ȃ��Ȃ��Ă��܂��܂��B������͂�����Ő��k�̂��Ƃ��l���Čv��𗧂ĂĂ���̂ł����A���k���g���W�����܂ł̑S�Ȗڂ̕��X�P�W���[���𑁂߂ɗ��ĂĂق����Ǝv���܂��B
���Z�R�N���̂P�N�Ԃ͖{���ɂ����Ƃ����Ԃł��B�v��𗧂ĂĎ��s���āA�����̖����P�N�Ԃ𑗂��Ăق����Ǝv���܂��B
�T���Q�O���@���z�̕��̎d��
����A���k���w�Z�̐搶��
�u���łP�x��������肪�o���Ȃ����ē{���āA�������̂��ƌ������Ă����ł���B�v
�Ƙb���Ă����̂�
�u����ȕ��ɓ{��搶������Ǝv������ǁA�P�x���������Ƃ��o���Ȃ��Ɠ{��̂́A�P�x��������݂�Ȃ��o����Ǝv���Ă��邩��ŁA�������Ă���킯�ł͂Ȃ���Ȃ��́v
�Ɛ��k�ɂ͘b���܂����B
���́A��x�����Ă��������A���Ƃ͎�����l�ʼn��K���J��Ԃ��Đg�ɂ��Ă����Ƃ����̂����z���Ǝv���܂��B���̊w�Z�̐搶�́A���k�Ɏ����ЂƂ�ŕ����o����悤�ɂȂ��Ăق����Ă��̂悤�Ɍ����Ă���̂�������܂���B
���̂悤�Ȃ��Ƃ����z���Ƃ͎v���Ă��Ă��A���͂P���āA���Ƃ͐��k�C���ŏo����悤�ɂȂ邱�Ƃ͂��܂�Ȃ��Ǝv���Ă���̂ŁA�m�ł͂��������K��������悤�ɂ��Ă��܂��B
�������A������꒷��Z�ŁA��肷����ƕ��K�����Ċw�͂��L�т锽�ʁA�m�ւ̈ˑ��x�������Ȃ��āA�����ŕ��K����K�������Â炭�Ȃ��Ă��܂��\��������܂��B�w�Z�ł��m�ł��A���ɂ����Ĉˑ���������Ƃ����̂͂��܂肢�����Ƃł͂���܂���B
�m�ɒʂ��n�߂����́A���K�̎d������������A���̏K����t���邽�߂ɂ��������܂����A�m�ł̎w���͏��X�Ɍ��炵�āA����I�ɕ����Ă����Ă��炢�����Ǝv���Ă��܂��B
�T���Q�P���@�����ŗV��
�����A���k�����ƌ�ɋ����Ăق�����肪����ƌ����̂ŋ����Ă��āA���w�͖ʔ����ȂƉ��߂Ċ����邱�Ƃ�����܂����B
���₳�ꂽ���́A���͂ōl���邾���ł͓���A������x�m�����v���������ł����B
���̎��́A���̒l�ɂȂ�Ƃ������Ƃ͒m���Ă����Ȃ���Ή����Ȃ��˂Ƃ����b������ƁA
���k����
�u���Ⴀ�A���̈ꕔ���}�C�i�X�ɕς��A�l���ς���ĉ����Ȃ��Ȃ��ł����v
�ƐV���Ȏ��₪�o���̂�
���̂Ƃ��́A���̎��������ό`���đΏ����������ƁA���ό`�����Ă����܂����B
����ɐ��k����
�u���Ⴀ�A���̍�����������A�l���ς���ĉ����Ȃ��Ȃ��ł����v
�ƐV���Ȏ��₪�o���̂�
���̂Ƃ��́A�m���Ă����Ȃ���Γ�����ǂ��������ό`�����邱�ƂőΏ����������ƁA���ό`�����Ă����܂����B
��ނ͊�{�I�Ȗ�肾�����̂ł����A���̎�����ސ�������H�v�����肵�āA�����[�����ό`���o����Ƃ����b�Ɍq�����Ă����܂����B���̂悤�Ȑ����k�́u�ʔ����ł��ˁ[�v�ƌ����Ă��܂����B
���w�̕��́A���̂悤�ɁA��������Ƃǂ��Ȃ�낤�ƍl���Ċg�����Ă����Ƃ������ʔ������̂ł��B�̂��߂ɖ���������悤�ɂȂ�P�����K�v�Ȃ̂ł����A�������Đ��w�ŗV�Ԃ��ƂŁA���w���D���ɂȂ��āA�͂����Ă����Ƃ������Ƃ�����Ǝv���܂��B
�T���Q�Q���@���܂���
���w�Z�⒆�w�Z�̂Ƃ��ɂ悭�����o�����Ƃ�����l�ł��A���Z�ŋ}�ɕ����o���Ȃ��Ȃ�l�����܂��B���Z�̕��ɂ��܂����͌����Ȃ��Ƃ������Ƃł��B
�S�ẲȖڂɂ����Ē��w�Z�܂łƍ��Z�ł́A���̗ʂƎ����S���Ⴂ�܂��B�����������Ƃ������Ă������Ŏ��̌������Ȃ�����A���܂Œʂ�ʼn��Ƃ��Ȃ邾�낤�Ǝv���Ă��邤���ɏo���Ȃ��Ȃ��Ă��܂��̂ł��B�������A���܂Œʂ�ł͂����Ȃ��ƋC�Â����̂Ȃ�A�s���Ɉڂ��Ȃ��Ă͂Ȃ�܂���B
�ŋ߁A�����܂ł���Ă���悤�ɂƎw�����o���Ă�����Ă��Ă��Ȃ����k�����܂��B�S���̃m�[�g�𒀈�`�F�b�N���Ă����ł͂Ȃ��̂ł��܂����Ă���Ǝv���Ă��邩������܂��A�������Ă��܂��B
���������s�������܂Ŏ���Ă������ʂ��A����ł���Ƃ������Ƃ𗝉����Ȃ��Ă͂����܂���B�w�Z�ł��m�ł����܂����Ă���Ǝv���Ă���͎̂��������ł��B���������l�͓����{�ԂŁA���܂����������Ȃ����ƂɋC�Â����ƂɂȂ�܂��B
�m�ɒʂ����Ƃ����܂ł̎�����ς��邫�������ɂ��悤�Ǝv���āA�ʏm���Ȃ���Ή����ς��܂���B
��������������A���ǂ͂ǂ����Ŕj�]���Ă��܂��̂ł��B����͕������łȂ��A�Ȃ�ɂł������邱�Ƃł��B�����������Ƃ�������ɂ��Ăق����Ǝv���܂��B
�T���Q�R���@�U���̗\��
�U���̗\��\���A�b�v���܂����B
�R�N�����n�͒���l����������
�u�S�����ʂ̍u���v�u���w�V�̉��K�u���v�u���w�T�`�U�a�̉��K�u���v�ɕ����܂��B
�ǂ̍u���ɏo�Ȃ��邩�A�i�H�̂��Ƃ��܂߂ĂU�����{���ɖʒk���������Ǝv���܂��B
�o������薾�m�ȖڕW�������āA�Ă��}���Ăق����Ǝv���܂��B
�T���Q�T���@������
�U���̏��{�Ɍ����̂�����A�S�����܂Ői�܂Ȃ���A�����ŕ��������ނɂȂ鍂�Z�R�N���������̂ł͂Ȃ����Ǝv���܂��B���ނ��Ă�������撣�낤�Ǝv���Ă��鐶�k�����邩������܂��A�o������葁�����|�����Ă��炢�������̂ł��B
���ɋ�肾�ȂƊ����镪��́A�o���邾���������K�����č������Ă����Ȃ���Ȃ�܂���B��蕪���ׂ��Ă����A���Ƃœ��������������Ƃ��ɗ����̓x�������ς���Ă��܂��B�����o���邱�Ƃ������Ă���A�����̕��������̗ǂ����̂ɂȂ�\��������̂ł��B
���𑁂��n�߂������L�����Ƃ����̂́A�����邱�Ƃ��������ƂōX�ɏo����悤�ɂȂ�Ƃ����ʂ����邩��ł��B����͂R�N�������̘b�łȂ��A�P�A�Q�N���ɂ������邱�Ƃł��B������Ȃ����Ƃ���ł܂Ƃ߂Ă��̂ł͂Ȃ��A�o���������ȂƂ�������Ă����悤�ɕ��K�����Ăق����Ǝv���܂��B
���ɕ��������ނ��Ă���R�N���̐��k�ɂ͏m�̎��ƑO�ɗ��Ă�����āA���͈͂̌����߂��s���Ă��܂��B���k���ɋ��͈͂�����Ă�����A���Ԃ̓s���Ȃǂ�����̂ŁA���W�c�ŋ�������A�ʂŋ������肵�đΉ����Ă��܂��B
�W���ɕK���ɕ����ė͂�L�����߂ɂ́A���̂����Ɋ�b�I�Ȃ��Ƃ�g�ɕt���Ă������Ƃ���ł��B
�T���Q�U���@����
�T���͒���l����C�w���s�Ȃǂ�����A�Q�N�����S�������Ď��Ƃ����Ȃ��Ƃ��������������߁A�S���������Ƃ��́u�O�p���v�̎��Ƃ����āA�S������Ȃ��Ƃ��͕��K��������A���܂łɏK��������̔��W�I�ȓ��e����舵���܂����B
����A���W�I�ȓ��e�͎����������e�[�}�Ɏ��Ƃ������̂ł����A���Z���w�̒��ł�����l�����ɂȂ�܂��B���������������Ƃ���قǓ���Ȃ��̂ł����A���S�ɗ����ł��Ă��鐶�k�͂���Ȃɑ����Ȃ��悤�Ɋ����܂��B
�������̕����������Ƃ��́A�����������Ȃ��g����̂��A�Ȃ��K�v�Ȃ̂����A�o��������̓I�ȏꍇ���l���邱�Ƃŗ������Ă��炨���Ƃ��Ă��܂��B���������Ƃ��l����Ƃ��͈�ʓI�ɂ����l����̂ł͂Ȃ��A��̓I�Ȑ��ōl���Ă݂�Ƃ������Ƃ���ɂȂ�܂��B���w�͈�ʉ������߂�w��ł����A������[�߂邽�߂ɂ͎����I�Ȏv�l���K�v�ɂȂ�܂��B
�����I�Ȏv�l�́A���w�����Ɍ��炸���̉Ȗڂł��A�Љ�ɏo�Ă�����K�v�ɂȂ�\�͂ł��B����ʂ��āA���������\�͂����܂��Ă����Ηǂ��ȂƎv���Ďw�����Ă��܂��B

�T���Q�V���@�����Ȑl
�U�����{�Ɍ����̂����邽�߁A�^�����ɏ������Ă���m�������͓��̓I�ɐh�����ȓ��X�𑗂��Ă��܂��B
�o�������x��x�ꂽ�肵�Ăق�������܂��A���������Ă��鐶�k�̏������ł���̂ŁA���O�ʼn������K�Ȃǂ�����ꍇ�Ȃǂ́A���Ƃ̃R�}���ړ������đΏ���������A�R�}���������Ȃ��Ƃ��͒x��Ă��Ă�������Ɛ��������邱�Ƃ�����܂��B
�O��̎��Ƃ̎��ɂP�X��������̃R�}�̎��Ƃ��鐶�k���A���O�̉������K�Ŋw�Z���o��̂��P�X�����ɂȂ�Ƃ����̂ŁA�x��Ă�������C�����ė���悤�Ɍ����Ă����̂ł����A�P�X���Q�T���ɏm�ɗ��܂����B
�u�����́A�x����Ȃ������́v�ƕ�������A�u�Еt���⒅�ւ����}���Ŋ撣���ė��܂����v�ƌ����Ă��܂����B�x��Ă������ƌ����Ă��A����R�Ǝv��Ȃ��������Ɋ��S���܂����B
������Ȃ͉̂�������Ȃ����ƂȂ̂ŁA�x��Ă����S�ɗ��Ă��������̂ł����A�o�������w�͂����Ă���p������ƁA�M�����o����̂��m���ł��B
�T���Q�W���@���b
���Ɛ������Ęb�����Ă�����A�����܂����ł��܂��܂����B
�����w�Z����Ɋւ�������k�ŁA��w�@�ɐi�w������A�A�E������Ƃ����l�����������Ă��܂����B���������l�����Ƙb������ƁA�l�ňقȂ����̌��ɂ͂Ȃ�̂ł��傤���A���Z������w����Ɋ����邱�ƁA�A�E���Ďv�����Ƃ́A���オ�ς���Ă����ʓ_���������肷��悤�ł��B�F�A�����悤�ɔY�݂�ꂵ�݂������Ă���̂��Ȃ��Ǝv���܂��B
�b�����Ă��������邱�Ƃ��Ȃ��悤�Ȃ��Ƃł��A�b�����邾���ŋ~����C�����ɂȂ邱�Ƃ�����܂��B�����������݂����Ă����Ƃ����K��������܂����A�������N���̂��̂悤�ȑ��݂ɂȂ��Ƃ������Ƃ��K�����Ǝv���܂��B
�w�Z��m�Ŋւ���Ă���Ƃ��́A�N�ƕt���������������͕�����Ȃ��̂ŁA�o��͕s�v�c�Ȃ��ȂƊ����܂��B
�T���Q�X���@�����̗p�����i���Q���̏ꍇ�j
����A�m��K�˂Ă��Ă��ꂽ���Ɛ��́A���Q���̋����̗p��������炵���A���͋��Ȃ̕���A�ʐڂ̗��K�����Ă���悤�ł��B�ƂĂ��^�ʖڂŁA�v�����������ċ����Ɍ����Ă���Ǝv���̂ŁA���i���Ă��炢�����Ǝv���܂��B
������ǂ�ł��Ċw�Z�̐搶��ڎw���Ă���l�����邩�ǂ����͕�����܂��A�����̗p�����ɂ��ď����Ă����܂��B
���Q���̏ꍇ�͋����̗p�����͔N�ɂP��ƂȂ��Ă��āA�V���Ɉꎟ����������A���i����ƂX���ɓ���������܂��B
�ꎟ�����ł́A�y�[�p�[�e�X�g�ƏW�c���_�Ȃǂ�����A���Z�̏ꍇ�A�z�_�͈ȉ��̂悤�ɂȂ��Ă��܂��B
�P�O�O�_�F��ʋ��{�i���w�Z�͈̔͂̍��p�����Ёj�C���E���Ȗځi�@���Ȃǁj
�S�O�O�_�F���Ȗځ@�@�@�@�@�@�@�@�@�@�@�@�@
�R�O�O�_�F�W�c���_�C�ʐځ@�@�@�@�@�@�@�@�@�@
���v�W�O�O�_
�������A��w����ɕ������őS�����ɏo�ꂵ����A�N�C�O���͑��ɎQ�����ĊO���łQ�N�ȏ�{�����e�B�A���������Ă����ꍇ�Ȃǂ́A�W�O�O�_�Ƃ͕ʘg�ōő�T�O�_�܂ʼn��_����܂��B
���_���O�g�Ŕ������邽�߁A�̈�Ȃnj��X�̗̍p�g�����Ȃ��Ȗڂ̏ꍇ�́A���_�������ꍇ�͍��i����̂�����d�g�݂ɂȂ��Ă��܂��B�܂��A�W�c���_�Ɩʐڂ̔z�_���R�O�O�_�Ƒ傫���̂ł������f����s���̂��߁A�����Ɏ��Ԃ��������͐��Ȗڂł�����Ɠ_��������悤�ɕ������������i�̉\���������Ȃ�Ǝv���܂��B
�����́A�앶�ƖʐڂɂȂ��Ă��܂��B���۔���͈ꎟ�����̂Ƃ��̓_�����O�D�P�{���ĂW�O�_���_�Ƃ��Ċ��Z���č��v�ō��i�����܂�܂��B
�Q�O�_�F�앶
�Q�O�_�F�ʐ�
�W�O�_�F�ꎟ�����~�O�D�P
���v�P�Q�O�_
�ꎟ�����̔z�_�Ȃǂ̓z�[���y�[�W�Œ��ׂ��̂ł����A���������̗p�������Ă����Ƃ��͉��_�̏�����P�O�O�_�������悤�Ɏv���܂��B���̂悤�ɔz�_���͕ύX����Ă���\��������̂ŁA�����̔z�_�������ƕς���Ă��邩������܂���B�i�����̏��́A���i�����l�ɂ������ނ����邽�߁A��W�v���ɂ͏����Ă��܂���ł����B�j���_�̕��������۔���ɍ��E�����̂��ǂ����͕s���ł��B
�w�Z�̐搶��ڎw���l�������̗p�����ɕs���i�ƂȂ����ꍇ�͘Q�l�ƂȂ�킯�ł����A�������ɕ��������Ă���l�͏��Ȃ��悤�ł��B�s���i�ɂȂ����ꍇ�A�u�t����Ƃ������̂ɖ��O���ڂ�܂��B�����ɖ��O���ڂ�ƂR�����̐l���ٓ��̎����ɁA�u�t�g�Ƃ������̂����\�����̂Ŋw�Z����A�������āA�u�t�Ƃ��ē����Ȃ��琳�̗p��ڎw���Ƃ����̂���ʓI�ȗ���ɂȂ�܂��B
�ǂ̂悤�ɂ��āA���̍u�t��I�Ԃ��Ƃ����b�ł����A����͂܂����x�ɂ��܂��B
�T���R�O���@�w�Z�̍u�t�ɂȂ�ɂ�
����̑����ɂȂ�܂����A�w�Z���ǂ̂悤�ɂ��ču�t��I�Ԃ��ł����A�n�b�L�������Ă��܂��R�l�ł��B�R�l�Ƃ����ƕ������������悤�ȋC�����܂����A����͔��ɍ����I�ŁA�d���̖������������邱�ƂȂ̂ł��B
�u�t�Ƃ��ē����Ă���l�͊�{�I�ɂ͈�N�_��ɂȂ�܂��B���ʂ̉�ЂŌ����A�h���Ј��Ɠ����悤�Ȉ����ŁA�����Řg�����܂��Ă��܂��Η��N�x�͓����w�Z�œ������Ƃ��o���Ȃ��Ȃ�܂��B���߂ɑΏ������Ă����Ȃ��ƁA���������������Ȃ��Ȃ�܂��B
���̂��߁A���ɓ����Ă���u�t�̕��́A���Y�Z�̍Z�������N�x�̍u�t�̌��������Ă��Ă���邱�Ƃ��قƂ�ǂł��B���Z�̋����̐l�����́A���̋���ψ���ɂ���̂ł����A���̃x�[�X�͊e���Z�̍Z���̘b�������ō��܂��B���߂��o��O�ɍZ���������l���ɂ��Ă̏��������Ă���킯�ł��B
���N�A�P�����̘b�������ŁA�Z���̗͊W�ɂ���ė~�������������������ė���Ƃ������Ƃ�����悤�ł����A�����ƍu�t�̘g�͂ǂ̊w�Z��������x�ϓ��Ɋ���U���邱�Ƃ������悤�ł��B�����̘g�͋}�ȕa�C��A�\�����Ă��Ȃ��Y�x�̏ꍇ�������Ċm���ɖ��܂�܂����A�u�t�̘g�͑��߂ɓ����Ă����Ȃ��Ɩ��܂炸�A�ň��l��������Ȃ���ԂŐV�N�x���n�܂�܂��B�����Ȃ�ƁA����̕��S���傫�����̂ɂȂ�̂ł��B�����������R�������āA���N�x�ȍ~�������Ă����\���������u�t�o���҂ɂ͐���������₷���Ȃ��Ă���Ƃ����ʂ�����܂��B
�������A�R�l�ōu�t��I�ԗ��R�́A���ꂾ���ł͂Ȃ��A�ǂ̂悤�Ȑl�Ȃ̂����������Ă���Ƃ����_���傫���悤�Ɏv���܂��B
�u�t�͐���͂���܂��i���Z�̏ꍇ�A�����S�C�Ɩ��͏o���Ȃ��A�P�Ƃł̐��k�����͏o���Ȃ��j���A�w�Z�œ����ȏ�A���̋����Ɠ��l�Ɏ��Ƃ��s���A���k�̎w�������āA�����������܂��B�\�͂�K�����S��������Ȃ��l���A�Ă�ł���Ƃ����̂͊w�Z�Ƃ��Ă̓��X�N������܂��B�ł�����A������x�����l�ɗD��I�ɐ���������Ƃ����̂́A�����I���Ǝv���̂ł��B
�����I�ɋ��t�ɂȂ낤�Ǝv���Ă��邯��ǁA�����̗p�����ɕs���i�������ꍇ�A�����̕�Z�Ɉ��A�ɍs������A���Z����̒S�C�̐搶���]���Ă���Ζ��Z�ׂĉ�ɍs���Ƃ����̂͗��h�ȏA�E�����ɂȂ�܂��B
�������������ƕ��s���Ă���Ă����Ăق����̂͋��Ȃ̕��ł��B�̗p�����̂��߂Ƃ��������łȂ��A�u�t�Ƃ��Č���ɏo���Ƃ��ɁA���k�ɖ��f��������Ȃ����x���̊w�͂�ێ����Ă������Ƃ͍Œ���̃}�i�[���Ǝv���܂��B