�Z���^�[�������֑�w�Q���w���܂Ł@��w���w�w���i���Z���Ώہj�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Q�����R�s
 �@�@
�@�@
���L�E�\��\
��{���
�m�̏��
��{���
�m�̏��
�Q�O�P�W�@�U��
�U���P���@������
��������^�����̐��k�͌����̂�����܂��B�����ň��ނ̐��k���������ȏ�̑��ɐi�ސ��k������Ǝv���܂��B
�^�����ɏ������Ă��鍂�Z�R�N���͈��ނ���Ύ��R�Ɏg���鎞�Ԃ�������̂ł��ꂩ��K���ɂȂ��Ċ撣��͓̂��R�ł����A���Z�P�A�Q�N�������ꂼ��̗��ꂪ�ς��Ǝv���܂��B
�W�c�ŋ��߂�������������鐶�k������Ǝv���܂����A����Ƃ͕ʂɏ��������������l�I�ȓw�͂��ӂ�Ȃ��悤�ɂ��Ȃ��Ă͂Ȃ�܂���B
���Z�ł͒��w�Z�̂Ƃ��Ƃ͔�r�ɂȂ�Ȃ����炢���ƕ����̗����͓���ł��B�Z���������ɏ������Ă���l�͕�����������ɂȂ�Ȃ��悤�ɁA�����𗥂��Ċ撣���ĉ������B
�����R�O�N�U���P�����݂̐i�x��
�P�N���@�@�@���w�T�E�E�E�u�Q�����̃O���t�ƕ������v�܂ŏC��
�Q�N���@�@�@���w�U�E�E�E�u�ΐ����v�܂ŏC��
�R�N���a�@�@�u�W�����v�E�E�E120��܂ʼn����
�R�N���V�@�@���w�V�E�E�E�u�ϕ��@�v�̖ʐς̓r���i�}��ϐ��\���j�܂ŏC��
�U���R���@�Z���^�[�����̗��K
���Z�R�N���͂��ꂩ��Z���^�[�����Ɠ����}�[�N�^�C�v�̖͎����邱�Ƃ������Ă��܂��B
�Q�O�Q�O�N���狤�ʃe�X�g�ւ̈ڍs�ɔ����Ĕp�~�ɂȂ�Z���^�[�����ł����A�ߔN�̃Z���^�[�����͏o�����ǂ��A���k�̊w�͂�K�ɕ]���ł��Ă���Ǝv���܂��B
��̑O�̃Z���^�[�����́A�w�͂̍������k�͂���قǑ�����Ȃ��Ă������_�����Ă��܂������A���݂͂�����x���K���s��Ȃ��ƈ��肵�č����_����邱�Ƃ��ł��Ȃ������ɂȂ��Ă���悤�Ɏv���܂��B
��̓I�ɋC�����邱�Ƃ̈�Ƃ��Ď��Ԃ̊Ǘ�������܂��B���ɁA����A���w�A�p��ł͖��́u��Փx�v�Ɓu���ʁv�ō������鎎���ƂȂ��Ă��܂��B�͎��ł��{�Ԃł��u���Ԃ�����܂���ł����v�ƌ������k�����܂����A����͎��Ԃ̊Ǘ���������K���o���Ă��Ȃ������Ƃ������Ƃł��B
���̂悤�Șb������ƁA���Ԃ�����ӎ����Ă��܂������Ȃ̂ł����A���͂����Ă��Ȃ���Ύ��Ԃ������炠���Ă����͉����܂���B
�ł�����A�}�[�N�^�C�v�̗��K������Ƃ��ɂ͌`���Ɋ����܂ł͎��Ԃ̂��Ƃ͍l�����ɖ����������K�����āA���ꂩ�珙�X�Ɏ��Ԑ��������Ă����̂��ǂ��Ǝv���܂��B���ɁA���ꂪ���Ȑ��k���u���㕶�v��{�ԂƓ������Ԃŗ��K����̂͂P�P���ʂ���ł��ǂ��̂ł͂Ȃ����Ǝv���܂��B
�}�[�N�^�C�v�̖�肪������x������悤�ɂȂ邭�炢���͂������Ƃ����l�́A���������͎��Ԃ��ӎ��������K���s���悤�ɂ��Ă����܂��傤�B
�U���T���@�����̌��ꉻ
���Z�P�N���͐��w�T�̓�ł���Q�����̏ꍇ�����̉��K���s���Ă���̂ł����A�������Ă��鐶�k�������ł��B
���Z���w�������o����̂��͐��w�T�̂Q�����������o����̂��ɂ������Ă�A�Ƃ����ʏd�v�ȕ���ɂȂ��Ă���̂ŁA���Ԃ��������Ă���������Ɨ���������悤�ɓw�߂Ă��炢�����Ǝv���܂��B
���̕��삪���Ȑl�̒��ɂ́u���ɓʂ̂Q�����̍ő�l�̏ꍇ�����͂Q��ނŁA�ŏ��l�̏ꍇ�����͂R��ނ��v�Ƃ����悤�ɁA���ʂ��o���悤�Ƃ��Ă���l������̂ł����A���̂悤�Ȏ��g�ݕ�������͔̂��Ɋ댯�ł��B
��J�������Ƃ��Ă����U�@��g�ɕt���Ă������Ƃ���Ȃ̂ŁA���m�ł͂��̂悤�Ȏw���͍s���܂���B�O���t�̏ꍇ�����́u�O���t��͈͂��ǂ̂悤�ɓ����̂���������ǂݎ��v�Ƃ������Ƃ��ӎ�����悤�Ɏw�������Ă��܂��B
��̓I�ɂǂ̂悤�Ȃ��Ƃ��Ƃ�����
a ��萔�Ƃ��āCx �͈̔͂�\�����u2<x<a�v�C�ua<x<a+2�v�C�u2-a<x<2+a�v�ɂ�����@x �͈̔͂��ǂ̂悤�ɕω�������̂������t�i���{��j�Ő������Ȃ����B
�Ƃ����悤�Ȏ�������Ă��܂��B
�w���҂��猋�ʂ��������邾���ł͂Ȃ��A���k�������̌��t�Řb����悤�ɂȂ�Ɨ������[�܂�ƍl���Ă��܂��B
���w���C�}�C�`�L�єY��ł���Ƃ����l�́A���������Ƃ��ɐ��������������̂ł͂Ȃ��A���ꉻ���ė������邱�Ƃ��ӎ����Ă݂Ă͂ǂ��ł��傤���B
�U���U���@�x�N�g���̊w�ѕ�
���ݍ��Z�Q�N���̓x�N�g���̎��Ƃ��s���Ă���̂ł����A�m�ŋ����Ă����@�Ɗw�Z�ŏK������@���Ⴄ���Ƃ������Ɛ��k�������Ă��܂��B
����́A�w�Z�ŏK����@�Ƃ��������A���ȏ��ɍڂ��Ă����@�ƌ������������m���Ǝv���܂��B
�x�N�g���̕���͋��ɂ��鐶�k�������A�����g���w������̓x�N�g�������ł����B���̗��R�͋��ȏ��̉�@��g�ɂ��悤�Ƃ��Ă�������ł͂Ȃ��̂��Ǝv���܂��B���ȏ��̉�@�͑N�₩�Ȃ̂ł����A�{������O�ꂽ����ۂɂ͎g�����Ȃ��Ȃ����̂�����悤�Ɋ����܂��B
���͋����闧��ɂȂ��Ă���w������Ƃ͋t�Ƀx�N�g���̕��삪���̂��������ӂɂȂ�܂����B����̓x�N�g���̕�����J��Ԃ������钆�Łu�x�N�g���Ƃ͉����v�u�x�N�g����p���ĉ����o����̂��v�𗝉��o�������炾�Ǝv���܂��B
���̖�肾��������Ηǂ��Ƃ�����@�ł͂Ȃ��A��̖����������ƂŁu�x�N�g���Ƃ͉����v�Ƃ����{���𗝉��o����悤�ȉ�@��`�������Ǝv���Ă��܂��B
�Q�l�܂łɁ��͐��k���g�����Ȃ��ɂ͓�����ȏ��̉�@�ł��B
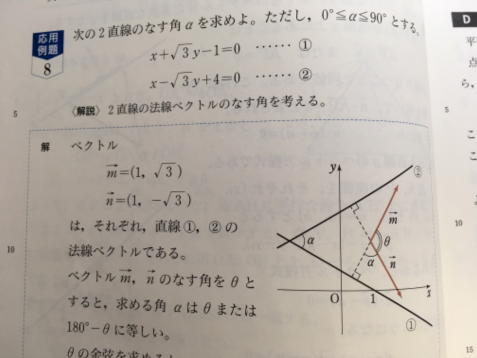
�U���X���@��Ղ̃��b�X��
NHK�Łu��Ղ̃��b�X���v�Ƃ����ԑg������̂ł����A����������Ă����u�싅�@�s�b�`���[�ҁ@�`�����f�B�E�W�����\���`�v���������ǂ������ł��B
�����W���[���[�K�[�̃����f�B�E�W�����\�������{�̒��w���ɃR�[�`�����Ă����̂ł����A���ʂȂ��Ƃ����������b�I�ȃo�����X��t�H�[�����ł߂邱�Ƃ̑����`���Ă����悤�Ɏv���܂��B
���ʂł͂Ȃ��ꗬ�ɂȂ邽�߂ɂ́A�n���ŒP���ȗ��K����j���O�ȂNJ�b���K��ӂ炸�ɍs��Ȃ��Ƃ����Ȃ��ƌ����Ă��āA���g�ގp���Ȃǂ��̏����ł͂Ȃ�������]��ł���悤�Ɋ����܂����B
�܂��A��{�I�ɂ͖J�߂Ă���̂ł����A�x�[�X�ނƂ��̑���ꏊ�ȂǁA�ׂ������Ƃł��o���Ă��Ȃ����Ƃ͉��̂������Ȃ��Ƃ����Ȃ��̂����R��������Ďw�E�����Ă��܂����B�����āA�w�E�������Ƃ��ɂ͏o���Ȃ��Ă��A�{�l�������Ƌ��ɏC�����Ă����̂��C���ɑ҂p���Ŏw�����s���Ă��܂����B
�싅�ɋ����������Ă��A���ł��X�|�[�c�ł��������邽�߂ɂ͋��ʓ_�����邱�Ƃ��w���͊w�ׂ�ł��傤���A�w���҂��w���̎d�����Ȃ݂邱�Ƃ��ł���ǂ����e�ł����B
�l�b�g�ŒT���Γ���͌�����Ǝv���܂��̂ŁA���Ԃ�������͐������������B
�U���P�O���@�����̃R�[�`�͎���
����̓��L�ɏ������u��Ղ̃��b�X���v�ł́u�싅�@�s�b�`���[�ҁ@�`�����f�B�E�W�����\���`�v�̘b�̒NjL�ł��B
�ԑg�̒��Ń����f�B�E�W�����\���́A�s�b�`���[�͎������Ƀ}�E���h��ŒN�������Ă���Ȃ�����A�����Ƀ_���ȂƂ��낪�������ɋC�Â��C�����邽�߂Ɏ����̃R�[�`�ɂȂ�Ȃ���Ȃ�Ȃ��Ǝw�������Ă��܂����B
����́A�싅�̃s�b�`���[�ȊO�ɂ����Ă͂܂邱�ƂŁA���������p����g�ɂ��邱�Ƃ͏d�v���Ǝv���܂��B
���Ō����ƁA�w�Z��m�ł͊�b�I�ȓ��e��g���[�j���O���@��`���邱�Ƃ͏o���܂����A��������ۂɐg�ɂ��邽�߂ɗ��K����͎̂������g�ł��B���̉ߒ��ŁA�~�X�����₷���Ƃ���◝�����\���ł͂Ȃ��Ƃ���͂��A�������邽�߂ɂ͉�������Ηǂ��̂����l���Ď��s���邱�Ƃ���ł��B
�w�������Ă���ƋH�Ɍ��I�ȐL�т������鐶�k�����܂����A�����������k�͎������g�ɍ��A�����K�v�����l���čs�����Ă���悤�Ɋ����܂��B
���z�̎����ɋ߂Â����߂ɁA�������ׂ��Ȃ̂������I�Ȕ��f���o����悤�ɂȂ肽���ł��ˁB
�U���P�P���@�}�[�N�^�C�v�̖͎��̌�
���Z�R�N���̓}�[�N�^�C�v�̖͎����鎞���ɂȂ�܂����B���m�ł́A�͎����I������玩�ȍ̓_�̌��ʂ��L�����Ă�����Ă��܂��B
�_���┻��Ɉ���J���Ă��鐶�k�������ł����A�u�ԓI�Ȍ��ʂ�����قNjC�ɂ���K�v�͂���܂���B
�����_�ő�Ȃ̂́A�����o���Ă��ĉ����o���Ă��Ȃ��̂����m�F���邱�Ƃł��B�܂��A���Ԃ̊Ǘ��̎d���Ȃǎ����̌`���Ɋ���Ă������Ƃ��ӎ����Ă������Ƃ���ł��B
�Ⴆ�A���w�UB�̎������S�O�_�������Ƃ��܂��B���̌��ʂ���Ȃ̂ł͂Ȃ��A���Ԃ���������c��̂U�O�_�̂����A�ǂꂭ�炢�����������Ȃ̂����m�F���邱�Ƃ���ł��B
�����玞�Ԃ������Ă��c��̖�肪�����Ȃ��Ƃ����l�ƁA���Ԃ�������Ύc��̖�肪�S�ĉ�����Ƃ����l�ł́A���ׂ���������Ă��܂��B
��肪�������Ɏ��Ԃ��]���Ă���l�́A��b�I�ȓ��e�̔������K������Ƃ��Ɏ��Ԃ������ė������d�����Ȃ���Ȃ�܂��A�����邯��ǎ��Ԃ�����Ȃ��l�͊�b�I�ȓ��e�̗��K������Ƃ��ɑ������ӎ�����K�v������܂��B
��ʓI�ɁA�Z���^�[�����̐��w�ł͖�肪�����Ȃ��Ƃ��ɂ͎��Ԃ��]��̂ł����A��肪������悤�ɂȂ��Ă���Ǝ��Ԃ�����Ȃ��Ƃ�����ԂɂȂ�͂��ł��B
�͎��������ɂ͌��ʂ����A���̎������ǂ�������ԂŁA���ꂩ��ǂ̂悤�ɕ������Ă�������U��Ԃ�K�������܂��傤�B
�U���P�R���@�O�p���̃O���t
�r�����m���Ă������k�̌X���Ƃ��āA�O�p���̃O���t�����ɂ��Ă���i�O���t���`���Ȃ��j�l�������ł��B
�u���w�U�v�ŎO�p���̃O���t���K�����Ƃ��ɗ��K�͂���̂ł����A�O���t��`�������̖�肪�قƂ�Ǐo�肳��Ȃ����߁A���K�ŃO���t�̗��K�����邱�Ƃ����Ȃ��̂ł͂Ȃ����Ǝv���܂��B
�܂��A���ȏ���Q�l���Ȃǂ�����Ɓu���w�U�v�ŕ�������s�����������Ƃ��Ɂu�P�ʉ~�v��p���ĉ������@����������Ă��āA�O���t��p���ĉ������@�͕ʉ��Ƃ��Ď��グ���Ă��邱�Ƃ������悤�Ɏv���܂��B
�������A���̓��L�ʼn��x�������Ă���̂ł����A�O�p���̓O���t��p���ĕ�������s�������������@����{�I�ȉ�@�Ƃ���ׂ����ƍl���Ă��܂��B
���I�Șb�ɂȂ�܂����A���R�͂R����܂��B
�P�ڂ́u���ƕ������E�s�����̊W�v�͑S�Ă̊��ɋ��ʂ��Đ��藧�̂ŁA���̍l������g�ɂ��邽�߂ł��B
�Q�ڂ́utan�Ɓv�̕s������A��`�悪�P�����ȏ�̕������E�s�����́u�P�ʉ~�v�ōl���邱�ƂɓK���Ȃ�����ł��B
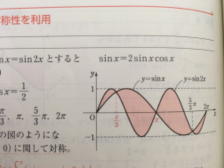
�R�ڂ̓O���t��`���K����g�ɂ��āu���w�V�v��u�����v�̃O���t�ɑΉ��ł���悤�ɂȂ��Ă��炢��������ł��B�Ⴆ�u���w�V�v�ł͉��̂悤�ȎO�p���̃O���t��`���čl�����肪�o�肳��܂��B
 �@
�@
���k���w�����鎞�ɂ́A�ڂ̑O�̖��̓����o�������ł͂Ȃ��A���w�𗝉����邽�߂ɂ͂ǂ̂悤�ɕ�������Ηǂ��̂����ӎ����邱�Ƃ�����ƍl���Ă��܂��B
�U���P�S���@�Ӗ��́u�����v�Ɓu�ËL�v
�u�Ӗ��̗L��i������j���t�v�Ɓu�Ӗ��̖����i������Ȃ��j���t�v���r�����ꍇ
�u�Ӗ��̗L��i������j���t�v�̕����o���₷���悤�Ɏv���܂��B
���͊w������Ɂu���E�j�v�Ȃǂ̎Љ���ł����B����́A�l����n���͈Ӗ��������Ȃ����Ƃ������̂Ŋo���邱�Ƃ���ɂ���������ł��B�܂��A�o�����̔w�i�𗝉������ɒP��݂̂��o���悤�Ƃ��Ă������߁A�m���Ƃ��Ē蒅���Ă��Ȃ������悤�Ɏv���܂��B
�������A�����悤�ɈËL�����Ȃ��Ƃ����Ȃ��p�ꂪ�����u�����v�͍D���ł����B����͌��t�ɈӖ���������̂������A���������邱�Ƃ��ËL�������Ă�������ł͂Ȃ����Ǝv���܂��B
����͐��w�ł��������Ƃ�������悤�Ɋ����܂��B
�����A���k���u�f�[�^�̕��́v�͈̔͂Łu���U�v�̌������ǂ����Ă��o�����܂���ƌ����Ă����̂ł����A�q�˂Ă݂�Ɓu���U�v�̈Ӗ��𗝉��o���Ă��܂���ł����B���Ȃ݂ɕ��U�̌����͈ȉ��ɂȂ�܂��B

���̌����̈Ӗ��͕�����Ȃ�����ǁA�l�Ă͂߂�Ɓu���U�v�����߂��邩��Ƃ肠�����o���悤�A�Ƃ������͋ꂵ���ł����ʔ�������܂���B
�u���U�v�̈Ӗ��͉����B�Ȃ��Q�悵�Ȃ��Ƃ����Ȃ��̂��B�Ȃ������n�Ŋ���Ȃ��Ƃ����Ȃ��̂��B�u�W�����v�́A�Ȃ��u���U�v�ɕ�����������̂��B�����ɂ͑S�ĈӖ�������܂��B
�����ŕ\���ꂽ���̂̈Ӗ��𗝉����Ă������Ƃ����w�̖ʔ����ł�����̂ŁA�����������Ƃ�`����ꂽ��ǂ��ȂƎv���Ă��܂��B
�U���P�U���@���K���܂��傤
�w�K���e��蒅�����邽�߂ɂ͒���I�ɕ��K�����邱�Ƃ��������܂���B
�����������̐��k�ɕ��K�����Ă��邩�q�˂��̂ł����A���M�������āu���K�����Ă��܂��v�Ɠ��������k�͂��܂���ł����B
���k�ɂ���Ă͕��K�̂������̂��悭������Ȃ��Ƃ����ӌ�������܂����B
��l��w���҂̊��o���ƁA���K�̂������炢�����ōl���Ď��s�ł��邾�낤�Ǝv���Ă��܂������ł����A���ۂɂ͓K�ɕ��K���o���Ă��鐶�k�͂���قǑ�������܂���B
�ƌ����킯�ō����́A�ǂ������S�\���ŁA�ǂꂭ�炢�̕��ʂ��A����p���ĕ��K����̂��Ƃ������Ƃ�������܂����B���e�͂����ɂ͏����܂����ʂȂ��Ƃ͌����Ă��܂���B
���܂ŐF�X�Ȑ��k�����Ă��܂������A���т��ǂ����k�قNJ�{�I�ȓ��e�̕��K���ɍs���Ă����悤�Ɏv���܂��B
�����o����悤�ɂȂ邽�߂ɂ͓��ʂȂ����������Ă��炤���Ƃł͂Ȃ��A��������Ă��Ηǂ���ƌ���ꂽ������O�̎���{���ɐM���Ď��s�ł��邩���Ǝv���܂��B
�U���P�V���@�ʎw���̃A���R��
���m�ł́A�ʎw���Ƃ��ċ��Ԃɖ����Ŏ��₪�o����悤�ɂ��Ă��܂��B
�z�[���y�[�W��TOP�ɍڂ��Ă���\��\�̉��F�����ԂɑΉ��\�ƂȂ��Ă��āA�\�����Ă��鎞�Ԃ͐Ԃ��Ȃ��Ă��܂��B
�w�Z�̏h��⎩���ŕ����Ă��ĕ�����Ȃ������Ƃ���Ȃǂ��P�A�Q�⎿�₷�邭�炢�ł���Η\�������K�v�͂���܂��A���␔������������A�P���̐��������ė~�����Ƃ��Ȃǂɂ͗\������ĂP���Ԃ���Q���Ԃقǎ��Ƃ����邱�Ƃ��\�ł��B
�w�Z�ɂ���Ă͐��w�̎��Ƃ��Q���蕡���̕���s���ċ����Ă��邱�Ƃ�����܂��B���������ꍇ�́A�Е��̕���͏m�Ő�s���Ď��Ƃ����邱�Ƃ��o���Ȃ��̂ŁA�w�Z�̎��Ƃŕ�����Ȃ������Ƃ���̎���ȂǂɎg���Ă��炤���Ƃ��z�肵�Ă��܂��B
��{�I�ɂ͉������₵�Ă�����Ă��\��Ȃ��̂ł����A��b�I�Ȃ��Ƃ������o���Ă��Ȃ��̂ɉ��p�I�Ȗ��̎��₵�Ă����ꍇ�͉�����s��Ȃ����Ƃ�����܂��B���̑���ɁA���̎��_�ł��Ȃ���Ȃ�Ȃ����Ƃ��w�����܂��B
������Ȃ��ł��炢�����̂́A��b�I�Ȃ��Ƃ𗝉����Ă��Ȃ��̂ɉ��p�I�Ȗ��̎�������Ă͂����Ȃ��Ƃ������Ƃł͂���܂���B���k�͖�肪������悤�ɂȂ邽�߂ɉ����K�v�Ȃ̂�������Ȃ����Ƃ�����܂��B
��Ȃ͖̂ڂ̑O�̖��̉�^���邱�Ƃł͂Ȃ��A������悤�ɂȂ邽�߂ɂ��ׂ����Ƃ��w�����邱�Ƃ��Ǝv���Ă��܂��B
�Ƃ����킯�ŁA���₵������������̂����������Ȃ�i�����ĕ��������������Ƃ������Ă��炦�Ȃ��j���Ƃ�����̂ł����A�ʎw�������p���ĉ������B
�U���P�W���@�n�k
�����A���n���ő傫�Ȓn�k������܂����B����̒n�k�ŖS���Ȃ�ꂽ�����o���͔̂��Ɏc�O�ŁA���Ɏ�҂��S���Ȃ����j���[�X�͐S���ɂ��Ȃ�܂��B
�ǂ�Ȃɔ����Ă��Ă��n�k�Ȃǂ̎��R�ЊQ�͖h���悤������܂���B��Q���邩�ǂ����͉^�̗v�f������̂�������܂��A�o��������Q�����������̂ɂȂ�悤�ɓw�͂͂��Ȃ��Ƃ����܂���B
���Q�����ł͐��N�O����Z�ɂ̑ϐk�H�����e�w�Z�ōs���Ă��Ă��܂��B�����N����Ȃ��Ƃ��ɂ͊�������Ƃł����A���������������v��I�ɍs���Ă���̂͂��肪�������Ƃł��B
�����̓��킪�N���ɂ���Ď���Ă��邱�ƂɊ��ӂ����āA�����̗͂��Љ�ɊҌ��ł���悤�ɓ��X�̓w�͂�ςݏd�˂邱�Ƃ�����Ǝv���܂��B
�U���P�X���@�����̕\�L�̎w��
�l�b�g�����Ă���Ǝ��̂悤�Șb��������܂����B
�����ŏm�̐搶�����Ă���l���A�w�������Ă��鐶�k�����w�Z�ňȉ��̂悤�ɐ����������悤�Ɍ���ꂽ�Ƃ����̂ł��B
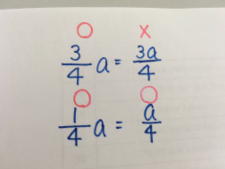
��������ƁA�����ƕ����̐ς͕��������ɏ����Ȃ���Ȃ炸�A���q�ɂ܂Ƃ߂ď����Ă͂����Ȃ��B�������A���q���P�̂Ƃ��͕����q�ɂ̂��Ă��ǂ��Ƃ������Ƃ炵���ł��B���̂悤�Ɏw�������闝�R�́A�w�Z�Ŏg���Ă��鋳�ȏ��̕\�L�����̂悤�ɂȂ��Ă��邩��Ƃ������Ƃ炵���ł��B
���̂悤�Ɏw�������邾���Ȃ炢���̂ł����A����ꂽ�ʂ�ɕ\�L���Ă��Ȃ����̂̓e�X�g�ŊԈႢ�Ƃ���Ɛ錾���ꂽ���ƂɁA�m�̐搶���{���Ă���悤�ł��B
�������A������̕\�L�ł����w�I�ɊԈႢ�ł͂Ȃ��̂ŁA������ԈႢ�Ƃ���Ƃ����͖̂\�����Ǝv���܂��B
���Z�̕���ł��A�x�N�g���̕\�L�ŕ��c�����������Ƃ�����܂��B���ȏ��ł͍����̕\�L�ɂȂ��Ă���̂ł����A���m�ł͉E���̕\�L�Ōv�Z������悤�Ɏw�����܂��B����͂ǂ���̕\�L�ł����w�I�ɂ͊ԈႢ�ł͂Ȃ��A��X�̂��Ƃ��l����ΉE���ŏ����K�������������ǂ��̂ł����A��͂苳�ȏ��ɍڂ��Ă��Ȃ��Ƃ������R�ŃN���[����t�����邱�Ƃ�����܂��B
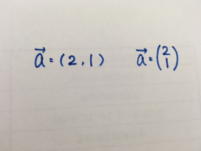
�������������̕\�L���߂�����́A���w�Z�́u�����鐔�Ƃ������鐔�v����n�܂��āA���܂Ōo���Ă������Ȃ�Ȃ��悤�Ɏv���܂��B
���̌����́A�����鑤�̘����ƁA���Ў�`�ɂ���̂ł͂Ȃ����Ǝv���܂��B
���k�ɕ��������Ă���ƁA�w�������鑤���D�ʂɗ����Ă���ƍl���Ă��܂����Ƃ�����܂��B���t�Ƃ����̂͋C�����Ȃ���A�����ɂȂ�댯�������闧�ꂾ�Ƃ������Ƃ�Y��Ă͂����܂���B
���ꂪ�s���߂���ƁA�����̋����Ă��邱�Ƃ͑S�Đ������āA�����������Ă��Ȃ����Ƃ͑S�ĊԈ���Ă���Ƃ����l���ɍs�������Ă��܂��̂ł͂Ȃ����Ǝv���܂��B
�܂��A���̐������Ƃ������f�����ȏ��Ƃ������Ђɂ���ĂȂ����̂��Ǝv���܂��B
���ȏ��́A�o�ŎЂ₻��ɊW����w�҂̃`�F�b�N�������Ă���̂ŁA���炩�ɊԈ���Ă��邱�Ƃ��ڂ��Ă��邱�Ƃ͂قƂ�ǖ����ł��傤�i�ʂ̊w�҂���N���[�������邱�Ƃ͂���炵���ł����j�B
�������A���ȏ��ɍڂ��Ă��Ȃ����Ƃ��Ԉ���Ă���Ƃ����킯�ł͂���܂���B
���ʍ\����̊W��A����I�ȍl���A�܂��A�w�K�w���v�̂ɏ�����Ƃ������R����ڂ��Ă��Ȃ�����������A�w��I�ɂ͍ڂ��������ǂ����Ƃł��f�ڂ��Ă��Ȃ��\��������̂ł��B
�{���͂����������������w���҂������āA���k�̋^��ɓ�������A���ǂ����@��`����ׂ��ł��B
���k���w�����邱�Ƃ͎��Ȍ����~�������߂ł͂Ȃ��A���k�̂��߂ɍs���Ƃ����̂������ɂȂ���Ȃ�Ȃ��Ǝv���܂��B
�U���Q�O���@�������Ȃ����R
���N����Ɋւ��d�������Ă���ƐF�X�Ȑ��k�ɏo��܂��B
�w�Z�ɋ߂Ă����Ƃ��́A��������C�������Ă��w�Z�����߂�Ƃ������k�͂���قǑ�������܂���ł������A�m�̏ꍇ�͕�������C��������Ώm�����߂Ă��܂��Ƃ������k���w�Z���͑����悤�Ɋ����܂��B
�m�͎���̈ӎv�ŕ������ɍs���ꏊ���Ǝv���Ă���̂ŁA��������C�������l�����߂Ă��܂��͎̂d�����Ȃ��Ǝv���Ă��܂��B
�����A�m���n�߂Ă��牽�N���o���܂������A����܂œ��m���ɕ�������C�������Ă��m�ɒʂ����������k�����Ȃ�����܂���B
�����������k�́A��������C�����������͕̂��̂�����������Ȃ�������A���e��������Ȃ��������߂ŁA�����̂͌����ł͂Ȃ��Ƃ����X�����������悤�Ɏv���܂��B
�������闝�R�͐l�ɂ���ĈႢ�܂����A�������Ȃ����R�̂قƂ�ǂ́u������Ȃ��v���炫�Ă���̂ł͂Ȃ��ł��傤���B
�u������Ȃ��v����w�͂����āu����������v�܂ł����Ε��𑱂�����Ǝv���̂ł����A����������Ȃ����k����l�ł��̏�ԂɂȂ邱�Ƃ͓���Ǝv���܂��B
�u����������v�܂ł̓w�͂ɑς����Ȃ��ďm�����߂Ă��܂��ꍇ�͎d������܂��A�m�ɗ��Ă���Ԃ́A���Ƃ����̏�Ԃɂ��Ă�������悤�Ɋւ�肽���Ǝv���Ă��܂��B
�U���Q�P���@���N�̂��ƂȂ̂ł���
���ꂩ�����l��������܂����A���ꂪ�I���Ήċx�݂��߂��Ȃ�o������v��𗧂Ă�l������Ǝv���܂��B
���̏o�������̈�Ƃ��ăI�[�v���L�����p�X�ɍs�������鐶�k�����܂����A��w�̃I�[�v���L�����p�X�ɂ͍s���Ă��Ӗ��������̂ōs���Ȃ��ʼn������B
�����⑫�����Ă����ƁA��������w�̃I�[�v���L�����p�X�ɂ͍s���Ă��Ӗ�������܂���B
������w����ōl���Ă�����A�w��Z���E�ȂǂŎ����邱�Ƃ����܂��Ă���ꍇ�͍s���Ӗ��͂���Ǝv���܂��B
��������w�͒��w�E���Z�܂łƈ���āA�̃V�X�e����A�s��������w��K����������Ƃ͌���Ȃ��Ƃ����_������܂��B
����ȊO�ɂ����R�͂���̂ł����A���x�������Ă���̂ňȉ��ߋ��̓��L������p�ł��B
�`�`���p�@��������`�`
�I�[�v���L�����p�X�ɍs���Ă����̑�w�������ɍ����Ă��邩�ǂ����͕�����܂���B���Z�������̍u�`���Ă��A��w�ɓ����Ă���w�ԓ��e�𐳊m�ɒm�邱�Ƃ͏o���܂���B�܂��A�I�[�v���L�����p�X�̂Ƃ��Ɏ���ɂ���͍̂��Z���Ȃ̂ŁA��w�̎��ۂ̕��͋C��������܂���B
�����w�̋������畷�����b�ł����A��肽�����Ƃ����m�Ɍ��܂��ē����Ă����w���̕����A�z���ƈႤ�ƌ����đ�w�����߂邱�Ƃ����������ł��B��w�ɓ����Ċw�Ԃ��Ƃ͑���ɓn���Ă��āA���Z���̒i�K�ł����S�Ēm�邱�Ƃ͕s�\�ł��B��肽�����Ƃ������đ�w��I�Ԃ��Ƃ͑�ł����A��w�ł͎����̂�肽�����Ƃ��o���Ȃ��Ă��A�������䂩�����e��������p���������Ƃ��K�v�Ȃ̂��Ǝv���܂��B
������Ӗ����������R�Ƃ��āA�I�[�v���L�����p�X�ɍs�����Ƃ��Ă����i�ɋ߂Â����Ƃ͖����Ƃ������Ƃł��B��������w�̃I�[�v���L�����p�X�ɍs���Ƃ������k�́A�̃V�X�e�������Ă��Ȃ����Ƃ������悤�Ɋ����܂��B��������w������ꍇ�A��ʓI�ɃZ���^�[���������ē_�����m�肷��܂ŁA�����w�����܂�܂���B�܂�A�I�[�v���L�����p�X�ɍs�����Ƃ��Ă����̑�w�����Ȃ��Ƃ������Ƃ͉��X�ɂ��Ă���킯�ł��B
�I�[�v���L�����p�X�ɍs���ĈӖ�������̂́A���E�Ȃǂł��̑�w�����邱�Ƃ��m�肵�Ă���ꍇ�����ł��B����ȊO�̏ꍇ�́A�s���Ă��Ӗ��͂���܂���B
�Ō�ɁA�Q�A�R���I�[�v���L�����p�X�ɍs���ĕ������Ȃ��Ă��w�͂ɉe���������Ǝv����������܂��A�ɑ��鍪�{�I�ȍl�������Ԉ���Ă���Ƃ����_�ő傫�ȉe��������Ǝv���Ă��܂��B���i�ɋ߂Â����߂ɂ͕������邵���Ȃ��A���̖ړI�̂��߂ɒʂ��Ă���m���x�ނ��Ƃ͖{���]�|�ɂȂ��Ă���ƋC�Â��Ă��炢�����̂ł��B
�`�`���p�����܂Ł`�`
���ڌ��Ċm�F���Ȃ��Ă��A���w�ɍs�������Ǝv���悤�ȑ�w�͑S�ėǂ���w�ł��B
���Ⴂ���Ă͂����Ȃ��̂́A��������w�ɍ��i���邽�߂ɕK�v�Ȃ̂͊w�͂ł��B�����ɍs����������ƑI��ōs���ꏊ�ł͂Ȃ��A�I�������ɏ��������ē��w���錠����̂ł��B
�U���Q�R���@�V���A�W���̗\��\
�V���̗\��\�ƂW���̗\��\�i���j���s�n�o�y�[�W�ɃA�b�v���܂����B�W���̗\����i���j�Ƃ��Ă���͕̂ύX����\�������邽�߂ł��B
�W���͕����̎�����Ƒ����s�Ȃǂ̗\�肪����l������Ǝv���܂����A�����_�ł͕�����Ȃ����Ƃ������̂ł͂Ȃ����Ǝv���܂��B
���ꂩ��\��𗧂Ă�Ƃ��ɁA���ƒ�̓s�����m�ɍ��킹�Ă��������K�v�͂���܂��A�\�ł�����z������������Ώ�����܂��B�Ƃ����킯�ʼn��̗\��\��z�z���Ă��܂��B
���Z�R�N���͂W���̕�K���������Ԃ͏o���邾���m�ɗ��ċK�������������𑗂��Ă��炢�����ƍl���Ă��܂��B���̑��̊w�N�̐��k�ł��A�Ƃ��ƃ_���_���߂��������Ȑl�͎��K�������p���Ă��������B
�܂��A�l�̖ڂ������������W���ł���Ƃ����l�́A���ƒ��̋����ŋĂ�����̐Ȃ��g���Ă��\��Ȃ��̂ő��k���ĉ������B
�X�P�W���[���\�����Ă���������Ε�����܂����A�V���ƂW���̌㔼�͌ʎw���̎��Ԃ𑽂���邱�Ƃ��ł��܂��B
���m�́A���C�̂��鐶�k���ǂ��ɂ��������Ƃ����v���ʼn^�c���Ă��܂��B���ƃv���X�ʎw���ƂȂ�Ɩ����̂悤�ɏm�ɗ��邱�Ƃ�����܂����A�ʎw���͖����ł��̂ŁA���C�̂��鐶�k�ɂ͌����Ă���Ǝv���܂��B
�r�����m���Ă��鐶�k�͐��w�����Ȃ��Ƃ������̂ł����A�W���I�Ɏw�����o������Ԃ͂P�N�Ԃ̒��ł���قǑ�������܂���B
���k�{�l�Ɋ撣�肽���Ƃ����ӎv������Ό����_�̊w�͖͂₢�܂���̂ŁA����l���������B
�U���Q�U���@�������̊J������
���݁A����l�����̊w�Z���������߂P�R������m���J���Ă��܂��B
�������Ԓ��̎��Ƃ�������͂P�R������Q�Q���܂ŁA�����A���K�����J�����Ă��܂��̂Ŏ��R�Ɏg�p���Ă�����č\���܂���B
���Ƃ��s���Ă��Ȃ����ԑт͎�����t���Ă��܂��B���ƃR�}�������Ă��鎞�ԑтł��A�������╜�K�����Ă���R�}�ł���Ύ�����t���Ă��܂��B�ǂ̃R�}���Ή��\���͏m���ɓ`���܂��B
�w�Z�ɂ���Ă͍l�����Ԃ�����Ă���ꍇ������܂��̂ŁA�����������k�͕��K��������Ԃɂ��Ă��܂��B�����R�c�R�c�ƕ��K�����邱�Ƃ͑�ł����A�P�����i���Ĉ�C�ɕ��K������Βm���̐������o���܂��B
���k�ɂ���ď͈قȂ�܂����A�l�X�ȕ��@�ŏm�����p���Ă��炢�����Ǝv���܂��B
�U���Q�W���@�Ă̏���
�����O�̓��L�ɂ��������̂ł����A�ŋ߃p�\�R���̒��q�������A�d�������Ă���ʂ������オ��Ȃ����Ƃ��x�X����܂����B
���m�ł͎s�̂̋��ނ��g�p���܂����A�Ǝ��ɍ쐬�����v�����g�����ƂŎg�p���邱�Ƃ������A�܂��A���Z�R�N���̋L�q���K�͑S�Ď��삵�Ă���̂ŁA�p�\�R���ւ̈ˑ��x�͂��Ȃ荂���Ȃ��Ă��܂��B
�����A�V�A�W���̖Z���������Ƀp�\�R�����g���Ȃ��Ȃ��Ă��܂��Ă͎��Ƃ����������Ȃ��Ȃ�̂ŁA�V�����p�\�R�����w�����܂����B
�m�����߂Ĉȗ��ƂȂ�̂łT�N�Ԃ�̔����ւ��ƂȂ����̂ł����A�T�N�Ԃ��o���Ă���ƐV�����Ȃ��Ă��邱�Ƃ������A��������Ɋ���܂���B�܂��A�f�[�^�̈ڍs���T�N���������̂ŁA����炪���Ȃ��g����̂��m�F���s��Ȃ���Ȃ�܂���B
���݂͍l�����Ԓ��Ȃ̂Ŏ��Ƃ��������������Ă��邽�߁A�b���͂����������ƂɎ��Ԃ��g�������Ǝv���܂��B
����l�����I���Ήċx�݂��ڂ̑O�ł����A�Ă��}����O�ɂ�������ƌv��𗧂ĂėL�Ӌ`�ɉ߂�����悤�ɂ������ł��ˁB